1. Introduction
푸리에 변환은 푸리에 급수의 약점을 보완하기 위해 제안된 적분 변환이다.
→ 푸리에 급수에서 주기(T)를 무한대로 보내는 것임의의 입력 신호를 다양한 파수를 갖는 주기함수들의 합으로 분해하여 표현한다.
→ \(sin, cos\)이 주기 함수이며, 고주파부터 저주파까지 많은 대역을 원본 신호로 분리

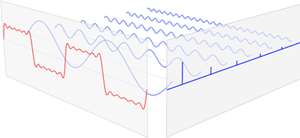
위 그림에서 붉은 색이 입력 신호, 파란색이 푸리에 변환 후 얻어진 주기함수 성분이다.
→ 성분들은 고유 주파수와 진폭을 지니고 있으며, 이걸 합치면 원본 붉은 신호여기서 입력 신호는 전파, 음성 신호와 같이 시간축이 정의될 수도 있으며, 이미지와 같은 상황에서 공간축으로도 정의될 수 있다.
통신, 음성 신호에서는 푸리에 변환을 time domain, frequency domain으로 변환하는 것을 의미하고, 영상처리에서는 spatial domain, frequency domain으로 변환하는 것을 의미한다.
2. Formulate


j는 허수이고, f(x)는 원본 신호 입력, \(e^{j2πux}\)는 주파수 u인 주기함수의 성분이다.
F(u)는 주기함수 성분의 계수(coefficient)를 나타낸다.앞 식은 입력 신호 f(x)는 \(e^{j2πux}\)의 합으로 표현(분해)된다. → 적분은 합한다는 의미를 가진다.
뒤 식은 f(x)를 주기함수 성분으로 분해했을 때 계수 F(u)가 위와 같이 나타남을 의미한다.위 주파수 그림과 연계하여, \(e^{j2πux}\)는 f(x)를 구성하는 파란색 frequency 주기함수 성분이고 F(u)는 이 주기함수 성분의 진폭을 나타낸다.
일반적으로 뒤 식이 푸리에 변환이라 정의하고, 앞 식이 푸리에 역변환이라고 정의한다.
주기함수 성분인 \(e^{j2πux}\)를 이해하기 위해 오일러 공식을 알아야 한다.

오일러 공식은 복소 지수 함수를 삼각함수로 변환할 수 있도록 하는 식이다.
위 식에 따르면 \(e^{j2πux}\)는 실수가 cos(2πux)이고, 허수가 jsin(2πux)인 주기함수다.
cos sin 둘 다 주기는 1/u이고, 주파수는 u이므로,
\(e^{j2πux}\)는 주파수 u인 sin파의 복소 지수 함수 표현이다.
※ 복소 지수 함수는 sin파를 표현하는 방법 중 하나
3. Discrete Fourier Transform


- 위 수식은 연속 Continuous, 아래 수식은 이산 Discrete
- DFT는 시간 영역의 이산 신호를 주파수 영역의 이산 신호로 변환하는 것을 의미한다.
또한 연속적이지 않고, 이들을 제외한 시간과 주파수에서 값이 0인 것을 포함한다. - 이산 시간에서는 데이터를 셀 수 있어 t 대신 number의 앞 글자 n을 사용한다.
(이산 시간에 대해서는 대문자 기호 사용) - 연속의 경우 음~양 무한대로 변화시키며 합을 계산하지만,
이산은 k가 0부터 증가해 계수 \(a_{k}\) 와 지수함수의 곱의 선형조합으로 합성방정식을 정의한다. - \(sin\)과 \(cos\)을 곱하는데, \(sin\)과 \(cos\)함수가 주기성이 있어 다른 정의역을 대입해도 같은 결과다.

4. Fast Fourier Transform

근사공식을 이용해 DFT를 계산할 때 연산 횟수를 줄일 수 있도록 고안된 알고리즘이다.
DFT의 경우 O(\(n^2\))의 시간 복잡도를 가지지만, FFT는 O(\(Nlog2N\))으로 상당히 빠르다.
DFT의 경우 n이 합성수일 때 소인수분해로 성능 향상이 가능하지만, FFT는 소수도 가능하다.

- 위 사진의 빨간 신호를 FFT하면 아래 사진의 파란 신호가 된다.
time domain이 frequency domain으로 나타내는 과정을 보인다.
5. Short-time Fourier Transform
FFT는 최종 길이를 전체에 대해 푸리에 변환을 하는 것과 다르게,
STFT는 최종 길이를 임의의 크기로 나누어 그 데이터에 푸리에 변환을 적용한다.

왼쪽의 경우, FT했을 때 주파수 외의 다른 정보를 얻기 어렵기 때문에 STFT를 활용한다.
신호를 window length에 따라 분리하여 FT에 사용되는 신호 길이를 감소시키고, 주파수의 resolution(분해능)이 악화된다.
6. Fourier series


- 어떤 파형이든 sin파 또는 지수함수의 합으로 표현 가능
\(a_{n}, b_{n} , c_{n}\) 은 파형을 가진 주파수의 성분

